El efecto túnel cuántico (I)

En un artículo aparecido en la revista Science, donde se analiza un estudio epidemiológico sobre las causas primigenias del cáncer en humanos, se obtiene la sorprendente (e ignorada hasta la fecha) conclusión de que casi dos tercios de los cánceres en humanos son consecuencia del puro azar, siendo las otras dos causas el ambiente (hábitos de vida, etc.) y la herencia como causa menor.

Obviamente, dado que el cáncer es una enfermedad celular, todas las causas del cáncer serán al final de tipo molecular (bien por errores de copia al fragmentarse el ADN en el proceso de división celular, bien por la existencia de agentes mutagénicos, físicos (radiaciones ionizantes) o químicos (radicales libres, moléculas carcinógenas, etc.). Por lo tanto, la Física Cuántica se encontrará en el fundamento de todas ellas. No obstante, esto es más determinante cuando las causas sonn estrictamente estocásticas, porque en este caso se trata de efectos cuánticos "puros". El principal responsable de las mutaciones aleatorias es el denominado "efecto túnel cuántico", que vamos a analizar cuantitativamente.

Preliminares clásicos.

Consideremos una partícula (problema unidimensional) moviéndose en una línea y sometida a un potencial de tipo "oscilador armónico": $V\left(x\right)=\frac{1}{2}k{x}^2$ (ver figura).

Dado que la energía cinética de la partícula de masa $m$ cumple que $T=E-V\left(x\right)\ge 0$, el movimiento de la partícula estará restringido entre los puntos $A\text{'},B\text{'}$, en que $V\left(x\right)\le E (T\ge 0)$. Será, en este caso una oscilación entre esos dos puntos, en los cuales la energía cinética es nula (y la energía potencial máxima). Esto es lo que se denomina un "pozo de potencial".

Consideremos ahora lo que se denomina "barrera de potencial" de altura $V_0$ y anchura $L$.
Una partícula con energía total

$E<V_0$

proveniente del infinito, a la izquierda, se moverá, aproximándose a $x=0$, con energía cinética $T=E$, pues

$V\left(x\right)=0, si x<0$

En $x=0$, su energía potencial será, justamente $E$, y su energía cinética nula. Invertirá el sentido de su movimiento, sin poder atravesar la barrera, dado que su energía total es inferior a la altura de la barrera.

Si, con el mismo tipo de movimiento, la energía total fuera superior a la altura de la barrera: $E\text{'}>V_0$, entonces podría atravesar la barrera, solo que mientras lo hace, su energía cinética sería $E\text{'}-V_0$, y no $E\text{'}$, emergiendo al otro lado de la barrera y prosiguiendo su movimiento con energía cinética $E\text{'}$.
En este último caso, efecto físico de la barrera sobre la partícula será el de retrasarla al atravesar la barrera, respecto de su movimiento (más rápido) si dicha barrera no estuviera.

Este es el paradigma clásico (para un campo de fuerzas conservativo). En el próximo artículo discutiremos y cuantificaremos su correlato cuántico, obteniendo una conclusión sorprendente y contraintuitiva; pero real. Tan real que es la responsable física última de un porcentaje significativo de los cánceres en humanos, y que además nos permitirá ejemplificar uno de los aspectos estocásticos de la Mecánica Cuántica.

Los orígenes de la Física Cuántica (IV)

El efecto fotoeléctrico.

Hacia 1905, Einstein, en su explicación del efecto fotoeléctrico (por la que recibió el Premio Nobel de Física) sugirió la naturaleza cuántica de la luz y la cuantización de la energía (en sistemas ligados).
El dispositivo experimental para el estudio del efecto fotoeléctrico (ver figura) consta de un circuito eléctrico con una batería, una resistencia variable, un voltímetro (no figura en la imagen), un amperímetro y una ampolla de vacío, en la que hay un cátodo metálico en un extremo y un ánodo metálico en el otro.

Luz monocromática (UV, por ejemplo) entra por una ventana de la cámara e incide en el cátodo, provocando la emisión de electrones. Algunos de estos electrones colisionan con el ánodo dando lugar a una corriente eléctrica entre las placas (la cual es medida por el amperímetro). La placa del ánodo está cargada negativamente, de modo que tiende a repeler a los electrones; solamente los electrones más energéticos la alcanzan.

La energía cinética máxima $K_{máx}$ de los electrones emitidos se consigue anmentando el voltaje hasta que la corriente se anula. El experimento muestra que $K_{máx}$ es independiente de la intensidad de la luz incidente, lo que contraviene a la Física Clásica pues, según ésta, al aumentar el ritmo al que incide la energía lumínica en la superficie metálica, la energía absorbida por los electrones de la misma debería aumentar, luego también la $K_{máx}$ de los electrones emitidos.

Pero experimentalmente se observa que $K_{máx}$ es la misma para una determinada longitud de onda de la luz incidente, con independencia de la intensidad de la luz (potencia por unidad de área iluminada).

La sugerencia de Einstein para explicar esta discrepancia fue que la energía luminosa debería hallarse cuantizada en pequeños "paquetes" llamados "fotones", siendo la energía de cada fotón:

$\boxed{E=hf=\frac{hc}{\lambda }} \left(1\right)$

Que es la ecuación de Einstein para la energía del fotón, en la cual

$h=6.626\times {10}^{-34}J·s=4.136\times {10}^{-15}eV·s$

es la constante de Planck, $f$ la frecuencia y $\lambda$ la longitud de onda.

Un haz de luz consiste, pues, en un chorro de partículas o corpúsculos cada uno de los cuales con energía $hf$.



El haz luminoso interacciona con la superficie del cátodo mediante colisiones fotón-electrón, en las cuales el fotón desaparece y cede toda su energía al electrón. Cada electrón emitido por la superficie metálica recibe su energía de un solo fotón.
Al aumentar la intensidad de la luz, lo que aumenta es el número de fotones incidentes por unidad de tiempo y unidad de área, y se emiten más electrones; pero como cada fotón tiene la misma energía $hf$, la energía absorbida por cada electrón también es la misma.

Si $\varphi$ es la energía mínima necesaria para arrancar a un electrón de un átomo de la superficie metálica, entonces:

$\boxed{K_{máx}=hf-\varphi } \left(2\right)$

Esta es la ecuación de Einstein del efecto fotoeléctrico. La magnitud $\varphi$ se denomina función de trabajo (trabajo o energía de extracción) del metal.

La ecuación (2) representa una línea recta ($K_{máx}$ en función de $f$), de pendiente $h$ y ordenada en el origen $-\varphi$.

Diez años más tarde del descubrimiento de Einstein, el físico norteamericano R.A. Millikan obtuvo un gráfico experimental de la ecuación (2), mostrando su corrección.

Observando el gráfico, inducimos que los fotones con frecuencia inferior a una frecuencia umbral $f_u$ (luego, respectivamente, con una longitud de onda mayor que una longitud de onda umbral ${\lambda }_u=c/f_u$) no tienen energía suficiente para expulsar a un electrón de un metal determinado.

De (2) deducimos:

$K_{máx}=0=h{f}_u-\varphi$

Luego

$\varphi =h{f}_u=\frac{hc}{{\lambda }_u}$

Se calcula que $hc=1240 eV·nm$ para los problemas, pues las longitudes de onda se suelen dar en nanómetros (nm) y las energías en electrón-voltios (eV).

EJEMPLO 1.- Considerando luz (espectro visible) de longitudes de onda entre $400 nm$ y $700 nm$, las energías de los fotones correspondientes a estos extremos, serán:

$\begin{array}{c}{E}_{400}=\frac{1240 eV·nm}{400 nm}=3.10 eV\\ E_{700}=\frac{1240 eV·nm}{700 nm}=1.77 eV\\ \end{array}$

Según estos cálculos, la luz visible contiene fotones con energías en el rango entre $\begin{array}{c}1.8 eV\end{array}$ y $\begin{array}{c}3.1 eV\end{array}$, aproximadamente.
Los rayos X están contituidos por fotones con energías del orden del $keV$. Los rayos gamma emitidos por los núcleos atómicos son fotones con energías del orden del $MeV$. Sus correspondientes longitudes de onda son

$\begin{array}{l}{\lambda }_X=\frac{1240 eV·nm}{1\times {10}^3 eV}=1.24 nm\\ E_{\gamma }=\frac{1240 eV·nm}{1\times {10}^6 eV}=0.0012 nm=1.2 pm\\ \end{array}$

EJEMPLO 2.- Conociendo que la intensidad de la luz solar en la superficie de la Tierra es aproximadamente $1400 \raisebox{1ex}{$W$}\!\left/ \!\raisebox{-1ex}{$m^2$}\right.$ y que la energía media de los fotones que llegan del Sol es de $2.00 eV$ ($\lambda \simeq 600 nm$), calculemos el número de fotones que inciden en un área terrestre de $1.00 c{m}^{\mathrm{2,}}$ en cada segundo.

Como $I=\frac{P}{A}=\frac{∆E}{A∆t}=\frac{Nhf}{A∆t}$ y $A=1.00 c{m}^2,∆t=1 s.$, se tiene que

$I=Nhf \left[\raisebox{1ex}{$W$}\!\left/ \!\raisebox{-1ex}{$c{m}^2·s$}\right.\right]$

Luego

$N=\frac{I}{hf}=\frac{\left(0.14 \frac{J}{c{m}^2·s}\right)\left(\frac{1 eV}{1.602\times {10}^{-19} J}\right)}{2.00 eV}=4.37\times {10}^{17}\frac{fotones}{c{m}^2·s}$

Los orígenes de la Física Cuántica (III)

Introducción matemática.

La distribución de Boltzmann de energías es un caso particular de distribución de una variable aleatoria del Cálculo de Probabilidades: la distribución exponencial (que a su vez es un caso particular de la distribución gamma).

De dice que una variable aleatoria $X$ sigue una distribución exponencial de parámetro $\theta$ (o que se distribuye según una exponencial de parámetro $\theta >0$, o que sigue el modelo probabilístico de una exponencial de parámetro $\theta >0$), y se escribe $X\hookrightarrow Exp\left(\theta \right)=\gamma \left(1,\theta \right)$, si su función de densidad es de la forma

$f_X\left(x\right)=\left\{\begin{array}{l}\theta e^{-\theta x}, si x>0\\ 0 , si x\le 0\end{array}\right.$

Es un cálculo integral sencillo el comprobar que la media o esperanza matemática de $X$ es

${\alpha }_1=\mathbb{E}\left[X\right]={\int }_0^{+\infty }\theta e^{-\theta x}dx=\frac{1}{\theta }$

integrando por partes.

DEFINICIÓN.- Una función $f:\mathrm{ℝ}\to \mathrm{ℝ}$ se llama función de densidad sobre $\mathrm{ℝ}$ si verifica:

(a) $f\left(x\right)\ge 0,\forall x\in \mathrm{ℝ}$.
(b) $f$ es integrable-Riemann en $\mathrm{ℝ}$ (esto es, el conjunto de puntos de discontinuidad de $f$ en $\mathrm{ℝ}$ es de medida de Jordan nula).
(c) ${\int }_{-\infty }^{+\infty }f\left(x\right)dx=1$.

Interpretación física de la función de densidad.

Sea $X$ una variable aleatoria continua con función de densidad $f_{X }y x\in \mathrm{ℝ}$ un punto de continuidad de $f_{X }$. Entonces, aplicando el Teorema del Valor Medio del Cálculo Integral, se tiene que

$\mathrm{\mathbb{P}}\left\{x\le X\le x+∆x\right\}={\int }_x^{x+∆x}{f}_x\left(x\right)dx=f_X\left(\xi \right)∆x,\xi \in \left[x,x+∆x\right]$

Como $\mathrm{\mathbb{P}}\left\{x\le X\le x+∆x\right\}$ representa una masa, si lo dividimos por $∆x$ (una longitud), obtendremos una densidad: $f_X\left(x\right)$. Luego $f_X\left(x\right)$ es la probabilidad por unidad de longitud, en el punto $x$.

En el caso físico que nos ocupará ahora, será $\theta =\frac{1}{kT}$.

Teoría de Planck de la cavidad radiante.

Para resolver la discrepancia entre la teoría (curva de Rayleigh-Jeans) y el experimento, Planck consideró la posibilidad de que la ley de equipartición de la energía (LEE), sobre la cual se fundamentaba la teoría anterior, fuera violada.
Asumiendo que $\underset{\nu \to 0}{\overline{\mathcal{E}}\to kT}$, en concordancia con los datos experimentales, propuso que $\underset{\nu \to \infty }{\overline{\mathcal{E}}\to 0}$.

La LEE asigna a $\overline{\mathcal{E}}$ un valor independiente de la frecuencia. La LEE procede, básicamente, de un resultado de la Mecánica Estadística conocido por la distribución de Boltzmann, que podemos definir aquí bajo la forma

$P\left(\mathcal{E}\right)=\frac{e^{-{\displaystyle \frac{\mathcal{E}}{kT}}}}{kT}$

Siendo $P\left(\mathcal{E}\right)$ la probabilidad de encontrar una entidad dada en un sistema, con energía en el intervalo $\left(\mathcal{E},\mathcal{E}+d\mathcal{E}\right)$, cuando el número de estados de energía para la entidad es, en ese intervalo, independiente de $\mathcal{E}$.

Se supone que el sistema contiene un gran número de entidades del mismo género, en equilibrio térmico a temperatura $T$. Las entidades que ahora consideramos en el sistema son un conjunto de ondas armónicas estacionarias en equilibrio térmico, dentro de la cavidad de cuerpo negro.
La distribución de Boltzmann nos ofrece completa información sobre las energías de las entidades en nuestro sistema. Su valor medio es

$\overline{\mathcal{E}}=\frac{{\int }_0^{+\infty }\mathcal{E}P\left(\mathcal{E}\right)d\mathcal{E}}{{\int }_0^{+\infty }P\left(\mathcal{E}\right)d\mathcal{E}}$

Entonces, integrando por partes, se obtiene

$\overline{\mathcal{E}}={\int }_0^{+\infty }\mathcal{E}P\left(\mathcal{E}\right)d\mathcal{E}={\int }_0^{+\infty }\mathcal{E}\frac{e^{-{\displaystyle \frac{\mathcal{E}}{kT}}}}{kT}d\mathcal{E}=kT$

Que es la ley de equipartición de la energía.

La gran y decisiva contribución de Planck fue suponer que la energía $\mathcal{E}$ es una variable discreta y no continua, con lo que el cálculo de $\overline{\mathcal{E}}$ se reduce al de la sumam de una serie numérica, y no a una integral impropia. Planck asumió que la energía $\mathcal{E}$ solo podía tomar valores discretos, uniformemente distribuidos:

$\mathcal{E}=0,∆\mathcal{E},2∆\mathcal{E},3∆\mathcal{E},\dots$

Si se toma $∆\mathcal{E}\ll kT$, se obtiene $\overline{\mathcal{E}}\cong kT$, pues el rango de energía $kT$ es mucho mayor que el incremento $∆\mathcal{E}$, y en la práctica $\mathcal{E}$ tiene una distribución que se diferencia poco de la continua.
Ahora bien, si $∆\mathcal{E}\approx kT$, no se puede ignorar el carácter discreto de $\mathcal{E}$ al evaluar $\overline{\mathcal{E}}$.

En resumen, Planck descubrió que se podía obtener $\overline{\mathcal{E}}\simeq kT$ cuando los incrementos $∆\mathcal{E}$ eran pequeños, y $\overline{\mathcal{E}}\simeq 0$ cuando los incrementos $∆\mathcal{E}$ eran grandes. Como era preciso obtener el primer resultado para valores $\nu$ pequeños y el segundo resultado para valores $\nu$ grandes, se precisaba que $∆\mathcal{E}$ fuera función creciente de $\nu$
Realizando cálculos, concluyó que la relación entre $∆\mathcal{E}$ y $\nu$ tenía que ser lineal, obteniendo experimentalmente la ecuación

$∆\mathcal{E}=h\nu$

siendo $h$ una constante de proporcionalidad (calculada experimentalmente, también), que se denominó después, en honor de su descubridor, constante de Planck:

$\boxed{h=6.6260693\times {10}^{-34}J·s}$

Derivación matemática de la expresión de Planck.

Por definición

$\overline{\mathcal{E}}=\frac{{\displaystyle \sum _{n=0}^{\infty }}\mathcal{E}P\left(\mathcal{E}\right)}{{\displaystyle \sum _{n=0}^{\infty }}P\left(\mathcal{E}\right)}$

Además, por el postulado de Planck: $\mathcal{E}=nh\nu ;n=0,1,2,\dots$.
Como $P\left(\mathcal{E}\right)=\frac{e^{-\frac{\mathcal{E}}{kT}}}{kT}$, se tiene

$\overline{\mathcal{E}}=\frac{{\displaystyle \sum _{n=0}^{\infty }}\frac{nh\nu }{kT}{e}^{-\frac{nh\nu }{kT}}}{{\displaystyle \sum _{n=0}^{\infty }}\frac{1}{kT}{e}^{-\frac{nh\nu }{kT}}}$

Escribiendo $\alpha =\frac{h\nu }{kT}$, se tiene

$\overline{\mathcal{E}}=\frac{{\displaystyle \sum _{n=0}^{\infty }}n\alpha e^{-n\alpha }}{\sum _{n=0}^{\infty }\frac{1}{kT}{e}^{-n\alpha }}=kT\frac{\sum _{n=0}^{\infty }n\alpha e^{-n\alpha }}{\sum _{n=0}^{\infty }{e}^{-n\alpha }}$

Pero

$\sum _{n=0}^{\infty }{e}^{-n\alpha }=\frac{1}{1-e^{-\alpha }}$

pues la serie anterior es geométrica, y como

$-\alpha \frac{d}{d\alpha }\left(e^{-n\alpha }\right)=n\alpha e^{-\alpha }$

se tiene que

$\sum _{n=0}^{\infty }n\alpha e^{-n\alpha }=-\alpha \frac{d}{d\alpha }\sum _{n=0}^{\infty }{e}^{-n\alpha }=-\alpha \frac{d}{d\alpha }\left(\frac{1}{1-e^{-\alpha }}\right)$

De los cálculos anteriores, se obtiene

$\overline{\mathcal{E}}=h\nu \frac{e^{-\alpha }}{1-e^{-\alpha }}=\frac{hv}{e^{\alpha }-1}=\frac{h\nu }{e^{\frac{h\nu }{kT}}-1}$

En conclusión

$\boxed{\overline{\mathcal{E}}=\frac{h\nu }{e^{\raisebox{1ex}{$h\nu $}\!\left/ \!\raisebox{-1ex}{$kT$}\right.}-1}}$

Los orígenes de la Física Cuántica (II)

Rayleigh y Jeans hicieron un cálculo de la densidad de energía de la radiación en el interior de una cavidad de cuerpo negro, el cual supuso un conflicto entre la Física Clásica y los resultados experimentales.

Consideremos una cavidad con paredes metálicas calentadas uniformemente a una temperatura $T$. Entonces, las paredes metálicas de la cavidad emitirán radiación térmica, en el intervalo térmico de frecuencias. Esto sucede, esencialmente, como consecuencia del movimiento acelerado de los electrones en las paredes metálicas de la cavidad, debido a la agitación térmica.

Usando la Teoría Electromagnética Clásica puede mostrarse que la radiación en el interior de la cavidad existe en forma de ondas estacionarias, con nodos en las superficies metálicas.
Calculemos el número de ondas estacionarias con frecuencias en el intervalo $\left(\nu ,\nu +d\nu \right)$.
Supongamos, por simplicidad, que la cavidad de paredes metálicas en cuyo interior hay radiación electromagnética, tiene la forma de un cubo de lado $a$. La radiación incidirá en cada pared opuesta y se reflejará en ella, pudiéndose analizar en tres componentes: uno por cada eje ortogonal del cubo. Al ser las paredes opuestas perfectamente paralelas, cada componente puede ser analizada independientemente de las demás.

Consideremos por ahora solo la componente $x$ y la pared metálica en $x=0$. Las radiaciones incidente y reflejada se mezclarán para componer ondas estacionarias. Como la radiación electromagnética es una vibración transversal, con el vector campo eléctrico $\mathbb{E}$ perpendicular a la dirección de propagación, $\mathbb{E}$ será paralelo a la pared. Pero en una superficie metálica no puede haber campo eléctrico paralelo a la misma (en caso contrario, las cargas libres del metal se moverían para compensar dicho campo y anularlo). En consecuencia, $\mathbb{E}$ para esta componente será el vector nulo. Luego la onda estacionaria asociada a la componente $x$ de la radiación, tendrá un nodo con amplitud $\mathbf{0}$ en $x=0$. Esto también ocurrirá en $x=\mathrm{a}$, por razones análogas. Y, de forma similar, para $y=0,a;z=0,a$.

Estas condiciones limitan las posibles longitudes de onda (luego las posibles frecuencias) de la radiación electromagnética en el interior de la cavidad.

Cálculo del número de ondas estacionarias en la cavidad, con longitudes de onda en el intervalo $\left(\lambda ,\lambda +d\lambda \right)$ (o, respectivamente, con frecuencias en el intervalo $\left(\nu ,\nu +d\nu \right)$.

Consideremos el problema unidimensional (de una cavidad unidimensional). El campo eléctrico de una onda electromagnética (OEM) unidimensional estacionaria viene dado por la expresión:

$E\left(x,t\right)=E_0\sin \left(\frac{2\pi x}{\lambda }\right)\sin \left(2\pi \nu t\right)$

Siendo $\lambda$ la longitud de onda de la OEM, $\nu$ la frecuencia, $E_0$ su amplitud máxima. Además, $\nu =\raisebox{1ex}{$c$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.$, siendo $c$ la velocidad de propagación de la OEM.

Como la función $\sin$ se anula para $\frac{2\pi x}{\lambda }=n\pi ,n\in \mathrm{\mathbb{Z}}$, se tendrá que

$\sin \left(\frac{2\pi x}{\lambda }\right)=0\iff \frac{2x}{\lambda }=n=0,1,2,...$

Y esto para todo instante de tiempo $t$.
Dado que la onda posee nodos en $x=0 y x=a$, se tendrá que $2a\raisebox{1ex}{$$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.=n,n=1,2,3,\dots$. Esta condición determina los valores posibles de $\lambda$.

Para las frecuencias, como $\nu =\raisebox{1ex}{$c$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.$, se deduce que: $\nu =\raisebox{1ex}{$cn$}\!\left/ \!\raisebox{-1ex}{$2a$}\right. , n=1,2,3,\dots$. Si representamos los valores de las frecuencias en diagramas en los que se marca un punto por cada valor de $n$, el valor de la frecuencia $\nu$ correspondiente a un $n$ particular será $\left(\raisebox{1ex}{$c$}\!\left/ \!\raisebox{-1ex}{$2a$}\right.\right)d$, siendo $d$ la distancia desde el origen a ese punto, o bien, $d=\left(\raisebox{1ex}{$2a$}\!\left/ \!\raisebox{-1ex}{$c$}\right.\right)\nu$. Luego el número de valores posibles de frecuencia, en el intervalo $\left(\nu ,\nu +d\nu \right)$ (número que denotamos mediante la expresión $N\left(\nu \right)d\nu$, será:

$N\left(\nu \right)d\nu =\frac{2a}{c}d\nu$

Como para cada frecuencia $\nu$ hay dos ondas (una por cada estado de polarización de la OEM), se tendrá:

$N\left(\nu \right)d\nu =\frac{4a}{c}d\nu$

para la cavidad unidimensional.
La extensión a una cavidad tridimensional es sencilla, numerando mediante $n_x,n_y,n_z$ para cada dimensión las componentes de la OEM tridimensional. El número de frecuencias posibles en el intervalo $\left(\nu ,\nu +d\nu \right)$ será igual al número de puntos contenidos entre celdas de radios correspondientes a las frecuencias $\nu$ y $\nu +d\nu$, que será proporcional al volumen contenido entre estos dos radios (debido a la distribución uniforme de los puntos $n_x,n_y,n_z$). Luego $N\left(\nu \right)d\nu \propto {\nu }^{2}d\nu$. Concretamente, se deduce que:

$\boxed{N\left(\nu \right)d\nu =\frac{8\mathrm{\pi }V}{c^3}{\nu }^{2}d\nu } \left(1\right)$

Siendo $V=a^3$ el volumen de la cavidad.

Una vez calculado el número de ondas estacionarias en el intervalo $\left(\nu ,\nu +d\nu \right)$, dentro de la cavidad tridimensional, evaluaremos la energía total media por cada onda de frecuencia $\nu$.

Según la Física Clásica, la energía de una OEM particular puede tener cualquier valor entre $0$ e $\infty$, siendo proporcional al módulo de la amplitud (del campo eléctrico) al cuadrado.

Para un sistema que contiene un elevado número de entidades físicas del mismo género, en equilibrio térmico, a temperatura $T$, la Física Clásica permite predecir el valor medio de la energía de esas entidades (en este caso, de las OEM estacionarias producidas por la radiación térmica de las paredes de la cavidad que se hallan a temperatura $T$). La llamada ley de equipartición de la energía reza: Para un sistema compuesto de un gas de moléculas en equilibrio térmico a temperatura $T$, la energía cinética media de una molécula, por grado de libertad, es $kT/2$, donde $k=1.38\times {10}^{-23}J/°K$ es la constante de Boltzmann.

Esta ley puede ser aplicada ahora, no a moléculas, sino a las ondas estacionarias en el interior de la cavidad (esto es, a cualquier gran número de entidades físicas del mismo género, en equilibrio térmico a temperatura $T$). Como cada onda estacionaria sinusoidal tiene una energía total que es doble de su energía cinética media, la energía total media de cada onda estacionaria será: $\overline{\mathcal{E}}=kT \left(2\right)$ (independiente de su frecuencia).

Ahora bien, la energía por unidad de volumen en el intervalo de frecuencias $\left(\nu ,\nu +d\nu \right)$, para el espectro de cuerpo negro del interior de una cavidad a temperatura $T$ es el producto de la energía total media por onda estacionaria y el número de ondas estacionarias en el intervalo de frecuencias $\left(\nu ,\nu +d\nu \right)$, dividido todo por el volumen de la cavidad. Luego de (1) y (2), se deduce:

$\boxed{{\rho }_T\left(\nu \right)d\nu =\frac{\frac{8\pi V}{c^3}{\nu }^{2}d\nu }{V}kT=\frac{8\pi {\nu }^{2}kT}{c^3}d\nu }$

La anterior es la fórmula de Rayleigh-Jeans para la radiación de cuerpo negro (ver figura).

Observando la figura, se comprueba la discrepancia entre la curva predicha por Rayleigh-Jeans mediante cálculos clásicos y la curva experimental. En el límite de bajas frecuencias, obsérvese que el espectro clásicamente predicho se aproxima al obtenido experimentalmente; pero a altas frecuencias, el espectro clásico diverge a infinito. Sin embargo, los experimentos muestran que la densidad de energía en el interior de la cavidad es siempre finita (como por otra parte es obvio) y que tiende a 0 a muy altas frecuencias.

El comportamiento irreal predicho por la Física Clásica a altas frecuencias se conoce en Física como la catástrofe ultravioleta, y sugiere un fallo de aplicación de la teoría física clásica, la cual ha de ser sustituida (mejor, extendida o ampliada) por otra.

En el próximo artículo veremos como, genialmente, Max Planck consiguió explicar el espectro observado de cuerpo negro de la cavidad radiante, lo que dio origen a la fascinante y ubicua teoría cuántica de la materia.

Los orígenes de la Física Cuántica (I)

El 14 de diciembre de 1900, en una reunión de la Sociedad Alemana de Física, Max Planck leyó los resultados de su investigación "Sobre la teoría de la ley de distribución de la energía del espectro normal".
Este documento, el cual atrajo poca atención, fue el inicio de una revolución en Física. La fecha de su presentación se considera el nacimiento de la Física Cuántica.

Radiación térmica.

Radiación térmica es la radiación emitida por un cuerpo como consecuencia de su temperatura. Todos los cuerpos emiten radiación a su entorno y la absorben o reciben de él. Si un cuerpo está más caliente que su entorno, la tasa de emisión de energía térmica excederá a la tasa de absorción de energía térmica, y el cuerpo se enfriará hasta alcanzar un equilibrio térmico con su entorno; en ese caso, las tasas de emisión y de absorción serán iguales.

La materia, en estados condensados (sólido o líquido) emite un espectro continuo de radiación. Los detalles del espectro son casi independientes de la composición del cuerpo; pero dependen fuertemente de su temperatura. A temperaturas ordinarias, muchos cuerpos son visibles no por la luz que emiten, sino por la luz que reflejan. A muy altas temperaturas, los cuerpos son autoluminosos. Pueden ser vistos en habitaciones a oscuras; pero incluso a tan elevadas temperaturas, el 90% de la radiación térmica emitida por ellos se encuentra en la región infrarroja del espectro electromagnético.
Cuando se incrementa la temperatura de un cuerpo, este emite más radiación térmica y la frecuencia de la radiación más intensa se hace mayor.

En general, la forma detallada del espectro de la radiación térmica emitida por un cuerpo caliente depende, en alguna forma, de su composición. Pero experimentalmente se comprueba que existe una clase de cuerpos calientes los cuales emiten espectros térmicos de carácter universal. Estos cuerpos se denominan cuerpos negros; es decir, cuerpos cuyas superficies absorben toda la radiación que incide sobre ellas.
Todos los cuerpos negros, a la misma temperatura, emiten radiación térmica con el mismo espectro. Este hecho puede ser explicado mediante argumentos clásicos relativos al equilibrio termodinámico. Pero la forma específica del espectro no puede ser obtenida únicamente mediante argumentos termodinámicos.

La distribución espectral de la radiación de un cuerpo negro se especifica por la magnitud $R_T\left(\nu \right)$, llamada radiancia espectral, la cual se define de tal forma que $R_T\left(\nu \right)d\nu$ es igual a la energía emitida por unidad de tiempo, mediante radiación de frecuencia en el intervalo $\left(\nu ,\nu +d\nu \right)$, desde la unidad de área de la superficie de dicho cuerpo negro, a temperatura absoluta $T$. 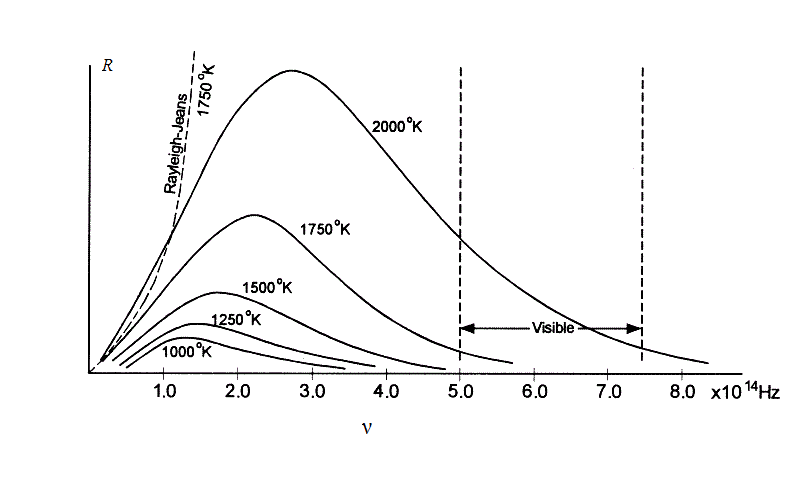La dependencia de $R_T\left(v\right)$, respecto de $v$ y de $T$ se muestra en la figura adjunta (para distintos valores de $T$).

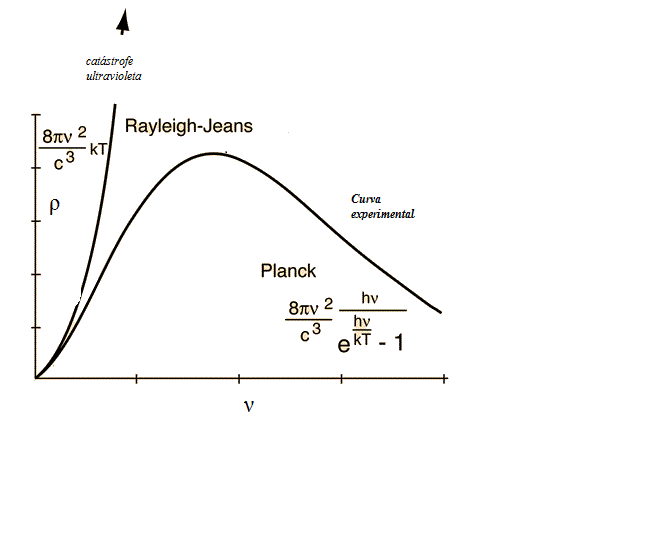
La distribución de la radiancia espectral de un cuerpo negro mostrada en la figura (para una temperatura determinada) nos informa de que:

a) La potencia radiada en un intervalo de frecuencias de amplitud fija $d\nu$ es muy pequeña cuando la frecuencia media del intervalo, $\nu$, es a su vez pequeña comparada con ${10}^{14}Hz$. La potencia es 0 para $\nu =0$
b) La potencia radiada en el intervalo $d\nu$ crece rápidamente desde pequeños valores.
c) Se hace máxima dicha potencia para un valor ${\nu }_T$, característico de cada temperatura y linealmente dependiente de ella; es decir, la potencia radiada es más intensa en esta temperatura y su valor para cada temperatura depende linealmente de esa temperatura.
d) Por encima de este valor característico ${\nu }_T$ la potencia radiada disminuye lenta pero continuamente cuando la frecuencia se incrementa. Se hace 0 de nuevo para valores $\nu \to \infty$.
e) La potencia total radiada en todas las frecuencias (área bajo cada curva de radiancia espectral) para una temperatura particular, se incrementa con la temperatura, y lo hace según la cuarta potencia de dicha temperatura:

${\int }_0^{\infty }{R}_T\left(\nu \right)d\nu$

Donde $R_T\left(\nu \right)d\nu$ es la potencia radiada en el intervalo de frecuencias $\left(\nu ,\nu +d\nu \right)$. Como $R_T\left(\nu \right)$ es la energía emitida por unidad de tiempo y unidad de área de la superficie de cuerpo negro, y por unidad de frecuencia, a la temperatura absoluta $T$ (en el S.I.: $\frac{W}{m^{2}Hz}$), entonces $R_T\left(\nu \right)d\nu$ será la energía emitida por unidad de tiempo (potencia) y por unidad de área de la superficie de un cuerpo negro a temperatura absoluta $T$, en el intervalo de frecuencias de amplitud $d\nu$.

Entonces, la integral (de Riemann) de la radiancia espectral $R_T\left(\nu \right)$ sobre todas las frecuencias, es la energía emitida por unidad de tiempo y por unidad de área desde un cuerpo negro a temperatura absoluta $T$, que se denomina radiancia, $R_T$, es:

$R_T={\int }_0^{\infty }{R}_T\left(\nu \right)d\nu$

Experimentalmente se comprueba lo que gráficamente se observa: que la radiancia de un cuerpo negro a temperatura absoluta $T$, sigue la siguiente ley de Stefan:

$R_T=\sigma T^4$

Donde $\sigma =5.6\times {10}^{-8}\left[\raisebox{1ex}{$W$}\!\left/ \!\raisebox{-1ex}{$m^2·°K^4$}\right.\right]$ es la llamada constante de Stefan-Boltzmann.

La figura nos muestra también que el espectro se desplaza hacia frecuencias más altas conforme aumenta la temperatura absoluta. Esto determina la llamada ley del desplazamiento de Wien: ${\nu }_{\text{máx}}\propto T$, donde ${\nu }_{\text{máx}}$ es la frecuencia $\nu$ para la cual $R_T\left(\nu \right)$ tiene un máximo relativo para una temperatura absoluta $T$.

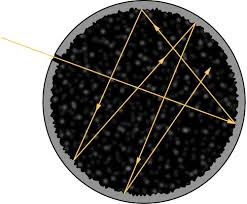
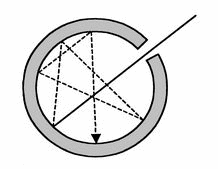
Un ejemplo de cuerpo negro es el de un objeto que contiene una cavidad conectada con el exterior a través de un pequeño orificio (pequeño comparado con la superficie exterior de la cavidad). La radiación externa que incida sobre la cavidad se reflejará varias veces en la pared del interior de la misma, siendo absorbida por ella. Luego el orificio tendrá la característica de un cuerpo negro. Si las paredes de esta cavidad se calientan uniformemente a una temperatura absoluta $T$, entonces las paredes de la cavidad emitirán radiación térmica, una parte de la cual (una muestra) emergerá por el orificio de la misma hacia el exterior. Como este agujero tendrá las características de la superficie de un cuerpo negro, el espectro de emisión emergente de la cavidad a través del agujero tendrá la forma del espectro de radiación de un cuerpo negro, y puesto que esa radiación emergente es una muestra de la radiación en el interior de la cavidad, esa radiación también tendrá el espectro característico de cuerpo negro a la temperatura $T$.

Para especificar el espectro de la radiación del interior de la cavidad, es más útil emplear la magnitud ${\rho }_T\left(\nu \right)$ (densidad de energía de la radiación en el interior de la cavidad), que el flujo $R_T\left(\nu \right)$. ${\rho }_T\left(\nu \right)$ es la energía contenida por unidad de volumen del interior de la cavidad a temperatura $T$ y en el intervalo de frecuencias $\left(\nu ,\nu +d\nu \right)$. Obviamente, ambas magnitudes serán proporcionales: ${\rho }_T\left(\nu \right)\propto R_T\left(\nu \right)$.

Como, para una onda electromagnética¹, $\lambda \nu =c$, siendo $c$ la velocidad de la luz, la ley del desplazamiento de Wien se puede escribir en la forma: ${\lambda }_{\text{máx}}T=const.$ Experimentalmente, el valor la de constante de Wien es $const.=2.898\times {10}^{-3}m·°K$.

Con estos datos podemos resolver algunos sencillos pero importantes problemas de Física.

PROBLEMA 1.- Si suponemos que la superficie de una estrellla se comporta como un cuerpo negro, podemos realizar una buena estimación de la temperatura de la misma. Para el Sol, ${\lambda }_{\text{máx}}=5100\stackrel{°}{\text{A}}$ y, para la Estrella Polar, ${\lambda }_{\text{máx}}=3500\stackrel{°}{\text{A}}$. Encontremos sus temperaturas superficiales.

$\begin{array}{c}{T}_{Sol}=\frac{const.}{5100\times {10}^{-10}m}=\frac{2.898\times {10}^{-3}m·°K}{5100\times {10}^{-10}m}=5700°K\\ T_{Polar}=\frac{const.}{3500\times {10}^{-10}m}=\frac{2.898\times {10}^{-3}m·°K}{3500\times {10}^{-10}m}=8300°K\\ \end{array}$

Haciendo uso de la ley de Stefan, calculemos la potencia radiada por cada $\begin{array}{c}c{m}^2\end{array}$ de superficie estelar:

$\begin{array}{c}{R}_{T,Sol}=\sigma T^4=5.67\times {10}^{-8}\frac{W}{m^2·°K^4}\times {\left(5700°K\right)}^4\cong 6000\frac{W}{c{m}^2}\\ R_{T,Polar}=\sigma T^4=5.67\times {10}^{-8}\frac{W}{m^2·°K^4}\times {\left(8300°K\right)}^4\cong 27000\frac{W}{c{m}^2}\\ \end{array}$

Obsérvese que, a $5700°K$, la temperatura de la superficie del Sol está próxima a la temperatura para la cual la mayor parte de la radiación emitida se encuentra en la región visible del espectro electromagnético. Esto sugiere que nuestros ojos se han adaptado, volviéndose más sensibles a aquellas longitudes de onda en las cuales el Sol radia con más intensidad.

PROBLEMA 2.- En una explosión termonuclear la temperatura de la "bola de fuego" es, momentáneamente, de unos ${10}^7°K$ (diez millones de grados Kelvin). Calculemos la longitud de onda de la radiación emitida con más intensidad.

${\lambda }_{máx}=\frac{const.}{T}=\frac{2.898\times {10}^{-3}m·°K}{{10}^7°K}=2.898\times {10}^{-10}m\simeq 0.3nm$

Esta longitud de onda corresponde a radiación gamma, como era de esperar.

PROBLEMA 3.- Suponiendo que la superficie del cuerpo humano se comporta aproximadamente como un cuerpo negro, calculemos la longitud de onda para la cual la radiación emitida por el cuerpo humano es máxima, considerando que este se halla a $310°K$ ($37°C$).

${\lambda }_{máx}=\frac{const.}{T}=\frac{2.898\times {10}^{-3}m·°K}{310°K}=9.35\times {10}^{-6}m~{10}^{-5}m$

Es decir, la radiación pedida está en el infrarrojo, como también era de esperar.

___________________________________________________________

¹ λ es la longitud de onda y ν la frecuencia de la onda electromagnética (supuesta monocromática).

El Principio de (No) Contradicción y la Mecánica Cuántica.

TEOREMA.- Un mismo sistema dinámico cuántico no puede estar y no estar a la vez en el mismo estado cuántico.

Demostración.- Sea S un sistema dinámico cuántico y |A〉 un estado cuántico de S. Estar S en |A〉 equivale a estar S en cualquier estado cuántico cuyo ket es de la forma c|A〉, siendo c un número complejo de módulo: |c| = 1.

No estar S en |A〉 ("estar S en no-|A〉") es estar S en un estado cuántico cuyo ket |B〉 es ortogonal al ket |A〉. Es decir, es estar S en un estado cuántico de la forma c'|B〉, con c' un complejo cualquiera de módulo 1, tal que

〈A|B〉 = 〈B|A〉 = 0.

Si S estuviese a la vez en A y en no-A, se cumpliría que

c|A〉 = c'|B〉             (*)

para ciertos números complejos c,c' de módulo unidad.

Luego

|A〉 = (c'/c)|B〉

y entonces el estado |A〉 de S es el mismo que el estado |B〉 de S, contra la hipótesis de partida. 

También, multiplicando escalarmente ambos miembros de (*) por el bra  〈B|  y realizando operaciones, se tiene


〈B|A〉 = (c'/c)〈B|B〉 = 0



Luego |B〉 = 0, lo que es imposible.

Q.E.D.

El Principio de Superposición Cuántico.

PRINCIPIO DE SUPERPOSICIÓN CUÁNTICO.- Si S es un sistema dinámico y |A〉, |B〉 son  estados cuánticos posibles de S, entonces

|R〉 = a|A〉 + b|B〉

es un estado cuántico posible de S, siendo a,b números complejos no nulos.

Hay una interpretación errónea de este principio toral de la MC, consistente en afirmar que estar el sistema S el estado cuántico |R〉, superposición lineal de los estados cuánticos |A〉 y |B〉, significa que el sistema S está a la vez en el estado cuántico |A〉 y en estado cuántico |B〉. Esto es, en general, incorrecto.

CASO 1. |A〉 y |B〉 son linealmente dependientes. Entonces existe un número complejo no nulo c, tal que |A〉 = c|B〉, y de ello se sigue que

|R〉 = a|A〉 + b|B〉 = a{c|B〉} + b|B〉 = {ac + b}|B〉

Es decir, el estado |R〉, el |A〉 y el |B〉 representan el mismo estado.

CASO 2. |A〉 y |B〉 son linealmente independientes¹. Entonces no existe ningún número complejo c tal que |A〉 = c|B〉, y el estado |R〉 es un nuevo estado de S, distinto de los estados |A〉 y |B〉.

Probemos que |R〉 es un estado distinto del estado |A〉, y por simetría quedará probado también respecto al estado |B〉. Si el estado |R〉 fuera igual al estado |A〉, existiría un número complejo no nulo c, tal que |R〉 = c|A〉.

Entonces, de

|R〉 = a|A〉 + b|B〉

con a,b no nulos, y de

|R〉 = c|A〉

con c no nulo, se deduce que

a|A〉 + b|B〉 = c|A〉

y operando en la igualdad anterior, se obtiene:

(a-c)|A〉 + b|B〉 = 0

Pero por la independencia lineal entre |A〉 y |B〉 se tendría, entonces, que

a-c = b = 0;

lo cual es imposible.

Y ahora viene el matiz que confunde al lego en MC. En las condiciones de independencia lineal entre |A〉 y |B〉 citadas, el carácter de "distinto" del estado |R〉 respecto de |A〉 y de |B〉 ha de ser entendido no como una distinción total, sino en el sentido en que, aun poseyendo el estado |R〉 algunas de las propiedades de los estados |A〉 y |B〉, no se identifica, en general, con ninguno de ellos, por ser un estado diferente (en general) de los mismos, según ahora matizamos.

DEFINICIÓN.- Sea S un sistema dinámico y |A〉, |B〉 dos posibles estados cuánticos de S. Definimos una medida de semejanza entre |A〉 y |B〉, de la siguiente forma:



En la ecuación anterior, ${∆}_{sem}\le 1$ es consecuencia de la desigualdad de Schwartz.

Entonces, diremos que los estados |A〉 y |B〉 son:

(i) completamente diferentes, si ${∆}_{sem}=0$.

(ii) completamente iguales o idénticos, si ${∆}_{sem}=1$.

(iii) ${∆}_{sem}$-semejantes, si ${∆}_{sem}\in \left(0,1\right)$.

Dichos estados serán más "parecidos" cuanto más próximo esté a 1 el valor de ${∆}_{sem}$.

En el caso (i), los estados |A〉 y |B〉 son ortogonales; esto es: 〈A|B〉 = 0.

__________________________________________________________________

¹También se define la independencia lineal entre |A〉 y |B〉 estableciendo que estos dos kets son linealmente independientes si para cualesquiera números complejos a,b, tales que a|A〉 + b|B〉 = 0, entonces a = b = 0.